Zemax光学设计实例（155）---一个柯克物镜的Seidel像差系数的计算

作者有话说：本文的计算还有些不完备的地方，欢迎多讨论、多指正。

引言：

Seidel像差系数中，五个单色三阶像差与两个一阶色差方程整合起来：

其中，A 等于ni ，i是近轴边际线的入射角度，A——等于 ni——，i——是近轴主光线的入射角度， h是近轴边际线的高度。H是 Lagrange不变量，等于nuh=n`u`h`。

还有，

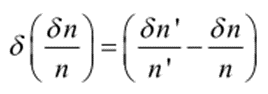
在光学设计中这七个公式非常重要。它们不仅简单易于理解，而且能够使设计者区分每个表面对特定像差的贡献量。

虽然，我们知道高级像差通常是限制镜头分辨率的主要因素，但是，对于一个具有好像质的镜头，校正以上七种像差却是必要条件。

柯克物镜seidel像差系数的计算过程：

以三片式的柯克物镜来举例，该实例来自ZEMAX自带的“Cooke 40 degree field”。

LDE结构参数如下：

2D Layout，如下图：

（1） 计算Lagrange不变量H

该柯克物镜的焦距是100mm，入瞳直径是20mm，即入瞳半径为10mm，这就是在入射面的边际光线高度，即h=10mm；

该柯克物镜的半视场角为20°，那么像的尺寸大小为100mm×tan20°=36.397023mm。

像方孔径角u`=h/f`=10/100=0.1

Lagrange不变量H=nuh= n`u`h`=1×0.1×36.397023=3.6397023

以上可以在ZEMAX MFE中直接计算与验证，如下图：

EFFL，有效焦距；

PARY，surf 1#，Py=1.0，第1面的近轴光线高度（注意：不要用REAY实际光线高度）；

PIMH，近轴像平面上的近轴像高；

DIVI，操作数5除以操作数6；

PROD，操作数3乘以操作数4；

以上从而计算得到Lagrange不变量H。

再用LINV直接计算Lagrange不变量H，两者结果一致。

（2） 追迹一条近轴边际光线

利用以下两个公式追迹一条近轴边际光线：

例如：计算第2面的近轴光线高度h₂。

第1面的近轴光线高度h₁=10mm，u₁=0，n=1.00，n`=1.6204，c₁=1/R₁=1/44.027185，d₁=6.517912。

n`、R₁和d₁的数据可以在ZEMAX LDE中得到，代入上面两式中可以求出h₂=9.433185mm。

可以在ZEMAX MFE中直接计算与验证，如下图：

两者计算结果一致。

由转面公式u₂=u`₁=-0.08696。

通过以上计算过程，可以依次求出各个面的u和h，列表如下：

可以在ZEMAX MFE中验证，如下图：

（3） 计算折射不变量A

对于近轴边际线，我们还可以计算折射不变量A：

由已知的n、h、c和u可以求出各个面的A，如下表：

（4） 计算每个面的球差系数S₁

其中，

由已知的n、n`、h、c、u、u`和A可以求出各个面的球差系数S₁，如下表：

具体计算过程，如下图：

再与ZEMAX Seidel Coefficient中的SPHA S1对比，如下图：

可以看出，该柯克物镜的球差系数S₁的计算结果基本一致。

（5） 计算每个面的轴向色差系数C₁

其中，

由已知的n、n`、v<sub>d</sub>、v`_d、h、和A可以求出各个面的轴向色差系数C₁，如下表：

具体计算过程，如下图：

再与ZEMAX Seidel Coefficient中的CLA（CL）对比，如下图：

可以看出，计算结果与ZEMAX给出的结果数值相同，符号相反。

（6） 计算每个面的场曲系数S₄

其中，

由已知的H、c和n可以求出各个面的场曲系数S₄，如下表：

具体计算过程，如下图：

再与ZEMAX Seidel Coefficient中的FCUR（S4）对比，如下图：

可以看出，该柯克物镜的球差系数S₄的计算结果基本一致。

（7） 求解每个面的离心率E

为了计算剩下的像差系数S₂、S₃、S₅、和C₂，我们需要每个表面的主光线折射不变量A——。

对于光学系统中的一些表面定义一个常量 E ， E 通常称为离心率，如下方程：

如此定义，那么E可以测出表面到光阑的距离，因为在光阑处的 h 为零。通常，系统中每个表面的 E 都不一样。

近轴主光线入射角度A——的表达式：

只要知道一个表面的近轴边际线数据（ h , u 和 A ）以及常量E ，就完全确定近轴主光线的数据。

假设已知光学系统表面i和1+i的近轴边际线高度，它们分别是h_i和h_i+1。

假设我们还知道表面i和1+i的近轴主光线的高度h——_i和h——_i+1。

推导得到

根据定义，在光阑处E为零，所以可以利用上式来计算靠近光阑表面的E，接着可以利用该式计算系统中的其他表面的E。

然后由各个表面的E就可以求出主光线的h——，u——和A——。

这个柯克物镜的第 4 个面是光阑面，即根据定义E₄等于零。

因为E₄等于零，那就有

同样地，由E₅可以求解E₆。至于光阑前面的表面，可以从光阑往前计算，先求E₃，然后求E₂，最后求E₁。

由已知的A、H、h和n可以求出各个面的E，h——和A——，如下表：

具体计算过程，如下图：

（8） 计算每个面的彗差系数S₂

其中，

由已知的n、n`、h、c、u、u`、A和A——可以求出各个面的彗差系数S₂，如下表：

具体计算过程，如下图：

再与ZEMAX Seidel Coefficient中的COMA S2对比，如下图：

可以看出，计算结果与ZEMAX给出的结果数值相同，符号相反。

（9） 计算每个面的像散系数S₃

其中，

由已知的n、n`、h、c、u、u`和A——可以求出各个面的像散系数S₃，如下表：

具体计算过程，如下图：

再与ZEMAX Seidel Coefficient中的ANTI S3对比，如下图：

可以看出，计算结果与ZEMAX给出的结果数值基本一致。

（10） 计算每个面的畸变系数S₅

由已知的S₃、S₄、A和A——可以求出各个面的畸变系数S₅，如下表：

具体计算过程，如下图：

再与ZEMAX Seidel Coefficient中的DIST S5对比，如下图：

可以看出，计算结果与ZEMAX给出的结果数值基本一致。

（11） 计算每个面的垂轴色差系数C₂

其中，

由已知的S₃、S₄、A和A——可以求出各个面的垂轴色差系数C₂，如下表：

具体计算过程，如下图：

再与ZEMAX Seidel Coefficient中的CTR（CT）对比，如下图：

可以看出，计算结果与ZEMAX给出的结果数值基本一致。

（12） 汇总

由这个柯克物镜的结构参数，计算得来的Seidel像差系数汇总如下表：

与ZEMAX的计算结果对比：

Seidel像差系数的汇总数据来看，球差S1、像散S3、场曲S4和垂轴色差C2的数值和符号都一致；但彗差S2、畸变S5和轴向色差C1的数值一致但符号相反。

应该注意的是，我们使用的是近轴数据来计算 Seidel 像差系数。这点对于初学者可能会产生困惑，即像差是由根据定义没有像差的光线（近轴光线）计算出来的。

计算 Seidel像差需要的所有变量都是近轴参数，即近轴边际光线以及近轴主光线的高度和角度。

Seidel像差只能适用于所有面都是standardsurface的系统。

利用Seidel像差公式可以分析镜头的像差特性，而光线追迹，还是很难给出这个分析。

Seidel像差系数的计算过程值得好好钻研，以充分理解这些方程的应用。