使用镜头模组的变焦镜头设计

摘要：本文给出了一种包含一阶和三阶特性的四组摄像机变焦系统的初始设计及其实际镜头设计。通过为每个镜组分配适当的一阶量和三阶像差，并结合优化所需的具体约束条件，得到了焦距长度范围为6.1693 ~ 58.4065 mm的最优初始设计。根据三阶像差理论，在给定共轭点上设计了一个真实的透镜来匹配一阶量和三阶像差，然后结合起来建立了一个实际的变焦系统。由各个设计组组合起来的系统，满足了由原镜头镜组组成的变焦系统的性能。利用后聚焦方法，得到了一种适用于视频变焦相机的变焦系统。

1. 介绍

       变焦镜头的设计通常分为两项任务。一是基于薄透镜的近轴研究【1-7】，给出每组焦距、变焦比、焦距范围、变焦轨迹等一阶参数等。二是从近轴研究和平衡像差出发建立变焦镜头系统。

       然而，这些方法有一些缺点。近轴研究得到的解决方案是否能够满足变焦镜头的所有要求，如封装约束、规格、总长度等是很难确定的。由于初始变焦镜头的像差没有得到纠正，所以在设计多组变焦镜头时，在所有变焦位置上的像差平衡需要更多的努力。

       由近轴分析和像差平衡引起的困难可以直接通过使用Stavroudis和Mercado【8】, Mercado和Stavroudis【9】, Kuper和rimmer【10】设计的透镜模组克服。透镜镜组是一个可以在不实际做详细设计的情况下建模一个复杂光学系统的数学模型。Kuper和Rimmer讨论的透镜模组基于模拟光线追踪，【11,12】，它包括通过一个由光程函数指定的透镜的追踪光线，而不是它的曲率，厚度或折射率.【10】。由于透镜组件是由一对共轭的所需成像特性所导出的光程来描述的，因此光程与波前像差之间的密切关系使得计算透镜组件的波前像差很容易。【13,14】

       透镜模组可以以多种方式用于光学设计。可以将它们用作设计一个真实的透镜，并根据可测量的量建模任意透镜，而不需要详细的规定。【10】使用透镜镜组设计变焦镜头具有以下优点: 模组可用于每个移动组和定义规范的参数，三阶畸变特性、变焦组的位置可以调整,以达到优化设计以及特定的约束。

       本文利用镜头镜组和三阶像差理论，给出了Tanaka提出的四组后聚焦变焦镜头的最优初始设计【15、16】，以及具体的约束条件，并从Seidel的实际镜头设计方案中得到了解决方案。每组的真实透镜都是根据模组的一阶和三阶像差进行分析设计的。然后将分别设计的组结合形成一个实际的变焦镜头。在平衡了高阶像差后，我们得到了一个宽视场极值f/#为1.65到窄视场极值f/#为2.95的变焦镜头，可以满足摄像机变焦镜头的所有要求。

1. 变焦系统的镜头镜组设计

       采用后聚焦方法【15.16】的四组变焦系统布局（如图1所示）。从物像方面看，变焦系统由固定的前镜头组、用于变焦的第二镜头组、固定的第三镜头组和用于对焦的第四镜头组组成。它们的分别表示为K1, K, K3, K4。第一组和第三组总是固定不变的。当第二组向右移动以获得更长的焦距时，第四组应移动以保持图像位置静止。

图1：四组后聚焦变焦系统布局图:(a)宽视场位置，(b)变焦位置，(c)窄视场位置

     当用于变焦的镜头组的位移为零时，即在位置1处，前一组的第二主平面(H’)与后一组的第一主平面(H)的距离由z11、z21、z31、z41指定，如图1所示。当第二组透镜位移最大时，即在位置3处，变焦系统有最长的焦距，位置2位于位置1和位置3的中间。如果一组从左向右移动，位移是正的。物方被设置为无穷远。

     每组一般由几个较厚的透镜元件组成，如图2(a)所示。在此图中，当忽略高阶像差时，厚透镜系统的特性可由其一阶量和给定共轭点的三阶赛德尔像差(包括瞳孔球差)来确定。换句话说，如果我们把透镜模组的一阶量和三阶像差赋给厚透镜系统，那么两个透镜在一阶和三阶性质的限制内是相等的。【10】因此,每组变焦系统都可以通过指定其焦距(FLM)、前焦距(FFM)、后焦距(BFM)、放大倍数(MGM)、入瞳位置(EPM)、入瞳直径(EDM)、视场角(β)和三阶像差来代替，如图2所示。

图2指定透镜系统所需的一阶参数:(a)一个厚透镜系统和(b)它的厚透镜镜组。

      我们已经建立由四个厚透镜镜组组成的后聚焦变焦系统（如图1所示），其中输入初始第一阶数作为一个变焦系统。它基于具有正光焦度的第一、第三和第四镜组和具有负光焦度的第二镜组。第二个镜组为负光焦度，假设每一组分别消色差。变焦系统的孔径光阑位于第三模组的前面，这样使系统在畸变平衡停止方面具有对称配置。它们之间的距离是1.5毫米，这足以保证安装空间。由于透镜模组不反映高阶像差，因此需要减小系统的孔径和视场大小，使三阶像差占主导地位。我们已经采取了半图像尺寸1毫米和f/#l的f/5在位置1到f/9在位置3变焦系统。

     所有变焦位置中，镜组之间的距离被限制超过0.7毫米。变焦时要避免镜组之间的碰撞，有安装空间。接下来，我们选择了尽可能短的总长度约束，以减少系统大小。在这种情况下，我们已经尝试总长度小于72毫米。当第二个镜组朝着一个方向移动以获得10倍的变焦比时，第四个镜组的位移量被限制在所有变焦位置上尽可能小。最后，我们在变焦时固定第一镜组的第二主平面与第三镜组的第一主平面的距离限制以及第三镜组的第二主平面与图像平面的距离。

     为了获得最佳的变焦系统，我们利用每个镜组的焦距、前焦距和后焦距、共轭点、间距和像差系数作为变量，优化了镜头镜组参数和特定的约束条件。我们很快得到了如图3所示的变焦系统。它的焦距为6.1693 ~ 58.4065 mm，像差得到了很好的校正，如图4所示。表1为各镜组的数据，表2为各位置的变焦轨迹。在表格1中。其中W040、W131、W222、W220、W311、W400表示边缘视场和出瞳处以d线波为单位计算的三阶波像差。因此，它们对应于球差、彗差、像散、Petzval曲线的波像差系数。畸变和瞳孔球差如表2所示。下标j表示变焦位置。

图3优化后的变焦系统，由四个镜头镜组组成。

图4:优化后的变焦系统由四个镜头镜组组成:(a)位置1和(b)位置3。

    表1:优化后变焦系统中镜头镜组的设计数据

表2:以毫米为单位的四个镜头镜组组成的变焦系统的一阶规格及变焦轨迹。

3透镜系统的一阶和三阶像差分析

     每组的设计采用三个透镜组成的全球面的厚透镜系统，即为表1中给出的厚透镜镜组。该透镜系统的原理图如图5所示。

     在该系统中，孔径光阑位于第一个表面(图5中的c)，主光线使与光轴的角度β位于孔径光阑。该系统的焦距f、前焦距、后焦距、给定共轭点的放大率、球差SI、彗差SⅡ、像散SⅢ、纵向色差SL、横向色差ST的三阶赛德尔像差系数用高斯括号表示为【17-20】

图5三片式厚透镜系统原理图。

     在这些方程中，kjj(j=1,2.，6)为每个曲面的光焦度，d j(j=1,2，…，6)为曲面间的距离。和u j(j=1.2....6)为光线与轴向物体点的会聚角，如图5所示。因此，光焦度k j由cj(nj-nj-1)给出，其中c j和n j分别为各表面的曲率和折射率。假设物体(n0)和像空间(n6)的折射率是一致的，方括号表示高斯括号。

      为使系统等效于厚透镜模组。在一阶和三阶性质的限制下，所有一阶量和包括孔径球差在内的所有三阶像差应等于透镜模组的一阶量和三阶像差。然而，同时处理所有的一阶量和三阶像差是非常复杂的。因此，在本文中，我们限制为四个一阶量和球差，彗差和像散匹配的透镜镜组。

      根据方程式(1)到(4)，则系统的焦距、后焦距、前焦距和放大倍率均等于透镜镜组的焦距、后焦距、前焦距和放大倍率，条件为：

其中，FLM、BFM、FFM和MGM分别是表1中给定共轭的镜头镜组的焦距、后焦距、前焦距和放大率，以及

同时,从方程式(5)、(6)、(7)为系统的球差、彗差和像散三阶像差系数等于透镜组件的这些系数，条件为

    其中，W040、W131、W222为表1所示透镜镜组的三阶波像差。因此。当我们忽略高阶像差时，(10)至(16)同时满足。除了佩茨瓦尔曲线、畸变、瞳孔球差和色差外，透镜系统等效于厚透镜镜组。预计方程 (10)、(11)、(12)和(13)可以很容易地解出来，但由于方程(14)、(15)、(16)是d3、C4、d4的高阶方程，求解过程十分复杂。

4. 每组解析解

      在变焦系统中，倾向于每一组分别消色差。然而，这需要另外两个等式。(8)和式(9)应为零，另行求解。本文用色差的解析估计来代替方程的求解。对于玻璃的选择，火石玻璃用于负光焦度元件，冕牌玻璃用于正光焦度。

      根据d1、d2、C1、C2和C3的适当初值，方程组(10)、(14)、(15)和(16)给出联立方程可由广泛的计算得到。【21】在这个过程中，设计参数d0, d3, c4, d4被确定。当它们被插入等式(11)、(12)、(13)时，系统剩余参数c5、d5、c6可确定。因此，通过在d1、d2、C1、C2和c3的适当范围内重复应用这一程序，等效透镜镜组的系统的赛德尔解的数值计算可得到。.

4.1 第一组

      变焦系统的第一个镜头组通常有一个双胶合透镜作为其前镜头【15,16,22,23】，这种结构有助于校正色差和彗差。然而，这意味着系统失去了两个参数，即曲率和厚度。通过在第一个曲面前面放置一个虚拟曲面，并将其参数c1和d1赋值为0。然而，这个系统可以被建模为一个由6个曲率和6个厚度组成的透镜系统。根据方程式(10)到(16)，便可找到赛德尔解。

       这些程序的结果如图6所示。图6(a)和6(b)分别说明了几个的纵向和横向色差随的变化。在这个图中，我们将距离d2设为1 mm，这足以构建变焦系统中直径最大的前镜头。从图6可以看出，该系统中不存在无色系统，其中玻璃为FDS9; BaCD14；BaCD14，对应透镜结构分别为负，正，正; 因此，我们要使R2和R3尽可能大，以得到一个色差较小的系统.

图6. d2=1时第一组透镜的分析:(a) 的变化，(b) ，它们作为给定R3的R2的函数(A, R3=25.5, b, R3=26.0, C, R3=26.5)

表3列出了由小色差赛德尔解选择的第一个透镜组的设计数据。对这个透镜和透镜镜组的评估I显示了预期的像差特性；也就是说，两个透镜之间的一阶量、球差、彗差和像散是完全一致的。

        表3第一组镜片以毫米为单位的设计数据。

4.2 第二组

       将具有强负光焦度的第二个透镜组建模为一个由单透镜和双胶合透镜组成的透镜系统。根据第4.1节描述的相同方法，第二组的Seidel解如图7所示。图7(a)和7(b) 分别说明了几个R3的纵向和横向色差随R2的变化。在这个图中， d2的解值是0.8毫米，这是一个合适的厚度。因为这个组有负的光焦度。玻璃的选择与第一组不同;也就是说，它们是TaF1，TaF1， FDS9三个透镜分别为负负正。从图7中，我们想使用曲线c上的解，如表4所示。

图7第二组镜片d2=0.8的分析: (a) 的变化，(b) ，它们作为R2的函数，对于给定的R3 (A, R=7.95: B, R3=8.0: C, R3=8.05)

        表4第二组镜片以毫米为单位的设计数据

4.3 第三组

      由三个分离的元素组成的第三透镜组的赛德尔解由如图8给出。曲线A和曲线B由  的正值的解。曲线B上的解C的绝对值比曲线C上的解C的绝对值要小，但在组合各镜头组得到的整个变焦系统中，前者的色差要比后者大得多。表5为曲线C上Seidel方案中选择的第三组设计数据。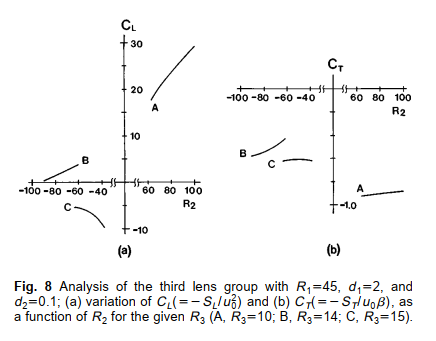

图8第三透镜组R1 =45, d1=2, d2=0.1的分析;(a) 的变化和(b) ，它们作为R2的函数，对于给定的R3 (a, R3=10, b, R3=14, C, R3=15)

      表5第三组镜片以毫米为单位的设计数据

4.4 第四组

        第四镜头组在像面上装有光学低通滤波器(OLPF)，用于滤除高频，提高CCD像面上的成像质量。由于OLPF是一个厚度为5mmm的平面平行板，假定其折射率与BK7的相同，因此会产生额外的像差。然而，已知的是，一个平面平行板引起的赛德尔像差在沿光轴移动时不变。它们实际上与入射高度无关。因此，我们可以把OLPF作为第四组的一个元素来处理，指定它的曲率为零，并通过等式给出联立方程(10)到(16)可以求解。图9显示了采用OLPF的第四组Seidel解，曲线C上选择的设计数据列于表6。

图9第四透镜组R1 =25, d1=2, d2=0.1的分析; (a) 的变化和(b) ，它们作为R2的函数，对于给定的R3 (a, R3=10, b, R3=11, C, R3=12)

       表6第四组镜片以毫米为单位的设计数据

4.5 完整的变焦系统

        根据表2中各位置的变焦轨迹，将第4节中单独设计的组进行组合，建立完整的变焦系统，如图10所示。表7给出了变焦系统的一阶参数(焦距，后焦距，前焦距)和变焦轨迹。两种变焦系统之间的一阶量已达成一致。图11显示了系统在两个极端位置的畸变。从图4和图11中，两种情况的比较显示出了预期的像差特性有少量的色差，畸变略大于透镜镜组设计，但在所有位置的球差都是相当好的结果。

图10从赛德尔方案中选择的组合组得到的变焦系统布局。

图11从Seidel方案中选择的组组合得到的变焦系统性能:(a)位置1和(b)位置3。

      在很多情况下，透镜模组的光学性能都超过了实际透镜，这并不奇怪。原则上，每个镜头镜组可以代表一个由任意数量的元素组成的非常复杂的镜头组。如果人们可以自由地改变实际设计中元素的数量，人们也可以期望它的性能可以得到改善。

       回到图10中的变焦系统，由于我们减小了光圈和视场的大小，三阶像差是主要因素，f/#太大，图像尺寸太小。为了满足当前视频变焦镜头【22】的要求，光圈和视场大小增加到在位置1达到f/1.65；在位置3达到f/2.95，且在所有变焦位置的半物高为3毫米。然而，在大孔径和视场系统中，以往设计中没有纠正的高阶像差变得非常重要。

      我们的目标是提高变焦系统的整体性能，扩大光圈和视场以满足变焦系统的要求。我们用一种简单的最小二乘法优化系统。以第4节和图10中获得的Seidel解为起点。在这个过程中，一阶布局，即所有组的焦距、变焦轨迹、所有位置的总长度都是固定的。在降低高阶像差时，我们特别注意使未校正像差失真最小化。

        经过多次迭代，我们得到了一个性能良好的变焦系统。系统布局如图12所示，其一阶特性与起始透镜相同。图13为残余像差，图14为系统的调制传递函数(MTF)特性。畸变得到显著修正，系统在全视场的变焦位置在50 lp/mm的MTF值超过40%。此外，该系统在全视场所有位置的相对照度都超过30%。因此，该系统具有足够的性能满足当前视频变焦系统的要求。

图12优化后的变焦系统布局，位置1- f/1.65到位置3 -f/2.95，半像尺寸为3mm。

图13：优化后变焦系统的残余像差:(a)位置1和(b)位置3。

图14优化后变焦系统的MTF特性:(a)位置1和(b)位置3。

6 结论

      本篇文章从镜头镜组的特性出发，建立了4个大口径、小视场的厚镜头镜组的变焦系统，并对其进行了优化。通过将各镜组的一阶量和三阶像差分配到特定的约束条件下，得到了变焦比约为10×的最优初始设计。

       利用三阶像差理论，通过匹配镜组在给定共轭点的4个一阶量和3个三阶像差，得到了每组真实透镜的赛德尔解。在解析解中选择了色差较小的透镜。然后我们将分别设计的小组结合起来，建立了一个实际的变焦系统，发现该系统在缩小光圈和视场时几乎相当于由四个镜头镜组组成的变焦系统。两种镜头之间的一致性很好；然而，由于扩展孔径和视场中存在高阶像差，仅使用三阶输入很难实现完美的一致性。因此，我们希望使用一阶和三阶输入在缩减区域设计初始系统，然后扩展系统以满足我们的目标。

       通过平衡增大孔径和视场中的高阶像差，进一步提高了其性能，保持其一阶布局不变。该系统宽视场极值光圈为f/1.65，窄视场极值光圈为f/2.95，半像尺寸为3 mm，变焦比约为10倍。这里设计的变焦系统很适合作为一个视频摄像机变焦系统表现得很合理。

       因此，使用镜头镜组的变焦系统的设计被分解为单个组的设计和组合的简单问题，并快速提供最优系统。