› 首页 ›资讯 › 查看内容

泽尼克单项式在宽视场光学设计中的应用

2021-12-14 14:41| 发布者：optkt| 查看：1724| 评论：0|原作者: 光学资讯

摘要：本文探讨了泽尼克单项式在宽视场光学设计中的应用，介绍了初级像差和像差节点的概念以及它们在光学设计中的重要性。同时，讨论了自由曲面镜在离轴系统中的作用。

综述

泽尼克多项式在波前光学建模和测试中具有普遍意义;然而，它们的多项式形式可能导致对单个像差的偏差。泽尼克多项式描述的波前轮廓包含多个具有不同阶数的孔径半径(ρ)项。泽尼克多项式是为使得RMS波前差最小和矩阵保持正交性由p项高阶和低阶组成的函数。

由于泽尼克和中仍然包含低阶多项式，因此单个单项存在非必要项。单次像差，也被称为赛德尔或初级像差，它在研究光学设计的复杂性、校正和场分布方面是适用的。光学设计软件报告的泽尼克多项式像差在大视场设计中并不代表单项像差，因为低阶多项式会被高阶项干扰。像差节点是单项像差为零的磁场位置。

本文给出了一种计算泽尼克多项式的矩阵方法（利用矩阵通过泽尼克多项式计算初级像差的方法）。初级像差作为视场角(H)的函数表示场阶(Hn)和实际像差节点的位置。相反，由于多项式的高阶和低阶项混合，泽尼克多项式与场(ZvF)图可以指出假像差节，。从泽尼克多项式转换而来的初级差节点理论，提供了光线追踪或实验室波前测量与节点像差理论(NAT)之间的联系。该方法适用于两种不同的光学设计:(1)120度圆形FOV鱼眼镜头和(2)120度*4度矩形FOV，离轴，自由四镜设计。

1.介绍

将泽尼克多项式拟合到波前作为视场角的函数，表明了剩余像差的类型，并提供了对设计[1]的单个像差平衡的见解。它也表明了表面形状在空间频率方面的复杂性。在轴对称系统中(例如:透镜)，许多泽尼克项为零。在这里，每个波前产生的唯一不对称是由于相对于光轴的不同视场角。从视场角度出发的波前仍然具有平面对称性。但是，在双平面对称设计中，YZ平面内已经存在不对称，所以y平面仍然具有平面对称性，而x平面会产生没有平面对称的波前轮廓。如下图1所示。上图中，对于轴对称透镜，波前的对称面用虚线表示。

与传统的折射系统相比，全反射光学系统有许多优点。如果全反射设计是离轴的，能够消除了传统反射望远镜的中心模糊，特别是在红外系统中，提升在图像质量和光通量方面优越性能。全反射系统的进一步好处是无限的光谱范围，较低的吸收和较低的热敏性。与传统的非球面或圆锥镜不同，自由曲面镜不围绕任何单轴对称，其表面形状是至少两个变量的函数。当在离轴系统中使用时，自由形镜增强像差控制。在宽视场(WFOV)全反射自由形式设计中，单个像差通过视场的变化很有意义，如图1(底部)中的例子，图2中有更多细节。这是一种离轴的、120*4度FOV、 f/3、 2.6英寸入瞳、0%畸变的四镜设计。

2.像差节点

在单透镜或反射镜中,视场相关的像差(例如:像散、慧差)与轴上无关只随视场（H）增而增加。然而,对于更复杂的和许多光学系统,离轴镜,或自由光学,在视场中可能存在像差形式为零的位置，称为像差节点。这些节点可以是点、线、圆或曲线。注意，像差节点并不意味着波前差或总像差为零。例如，在一个彗差节点上，彗差在该场点为零，但仍可能有像散、球差等。

在轴对称系统中(如:透镜)，像差节点是圆形的，是由相反符号的高阶和低阶像差导致的。例如，具有初级象散w222=0.1波和更高阶象散w422=-0.2波的透镜将在H=0.707处有一个圆形节点(归一化场半径)。

在离轴反射系统中，还有附加的像差，称为双侧对称像差[2]。这些像差可以具有与原像差相同的波前形状作为初级像差，但具有不同的视场角和方向性。波前的大小和方向是X方向(对称平面内)视场的函数。也有双侧对称像差是视场无关的(常数)。例如，具有初级象散w222=0.2波和场常数象散w02002=0.1波的离轴反射镜系统将在HY= 0.707处有两个线节点(Y轴归一化的场)。

下图3所示的离轴镜系统(离轴三反系统)具有下图4所示的初级彗差二维视场剖面图。这里我们可以看到两个节点(图4右侧蓝色):一个是线性的，另一个是曲线的，初级彗差几乎为零。与图2的设计不同，图3中的反射三片式具有方形视场和更小的低阶像差，这允许Zemax的2DZvF图显示像差节点位置。

3.泽尼克多项式与单项

初级像差在其视场(H)和孔径(ρ)依赖是相关的。相反，泽尼克多项式包含多阶p，而不是H的函数。高阶泽尼克项是高阶和低阶的和，以减小该项的RMS波前差。随着波前变得越来越复杂，常见的WFOV系统需要更高阶的泽尼克多项式来准确描述波前。在拟合过程中调整低阶泽尼克多项式以适应高阶泽尼克多项式。然而，这导致了低阶系数即与初级像差相关出现误差的问题。

对于具有倾斜光学系统[2]的离轴系统，存在单项式双边对称像差的计算方程。然而，对偏心光学系统进行计算是非常具有挑战性的。另外，在光线追踪模型中，可以通过多项式拟合波前作为视场角的函数来测量单个像差。商业光线追踪软件(如Zemax和Code V)有计算泽尼克多项式系数与视场角的函数，称为泽尼克与视场(ZvF)。对于大多是低阶像差的系统，单个泽尼克系数可以准确地描述单个像差。例如，在单透镜中，泽尼克系数

给出了X轴上像散的精确大小。然而，对于更复杂的光学系统，离轴镜，或自由光学，有更高阶像差，低阶泽尼克方法不再能准确地描述单项像差。高阶泽尼克项也包含低阶项，当存在高阶像差时，高阶泽尼克项具有非零值。所以在某种意义上，泽尼克的高阶项掺杂了低阶项，但反之亦然。

由于泽尼克多项式项是低阶项和高阶项的和，这导致了解释单个(单项)波前形式(例如:像散、彗差、三叶草trefoil)的问题。以前的作者强调在1D或2D中绘制单个像差项和视场角的价值，使用泽尼克系数来找到像差节点[4,5]。然而，这些方法似乎不能正确地和高阶泽尼克项来产生一个只有的单次像差项。这些方法仅适用于没有高阶像差的简单光学系统。

单次像差的方法更类似于初级/赛德尔像差，但并不完全一样，因为初级像差没有关于X\Y(弧矢、子午)像散、三叶草等的术语。此外，原始像差描述了波前的视场相关性，而泽尼克项则不描述。例如，W220场曲率具有像那样的简单离焦的波前形状，但相反地给出了随视场变化的离焦大小[场曲率是随视场（H）二次增长的离焦，如H2]。

这个例子演示了结合泽尼克项来产生纯粹的单形式像差项(例如:像散只和p2相关，这里称为Wastig1)。水平面上表示像散的前三个泽尼克条项是(Z5, Z12, Z21)。请注意大写的“Z”是泽尼克多项式波前剖面，是p和φ的函数。小写的z是多项式系数。两者的单位都是波长。这三个多项式的像散可以总结为：

注意，限制全部的像散Z21是一个近似值。总的精度需要所有高阶泽尼克项的极限和。将泽尼克多项式系数转化为泽尼克单项像差的一般方程可以写成矩阵形式。先前的作者已经写出了标准泽尼克项的两个因变量（n,m）转换方程[6 - 8]。在这里，将带有一个因变量的单变泽尼克项写成更为简化的形式: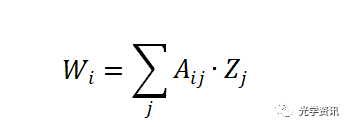

Wi是单项像差(例如:焦点、子午方向像散等)。

Zj为泽尼克系数的N1向量，由泽尼克拟合软件(如Zemax)输出。

Aij为转换矩阵，其中i为特定单项像差Wi对应的行，j为每个泽尼克系数的列。这个矩阵的一部分如表1所示。

转换矩阵为稀疏（矩阵），因为大部分元素都是零。由于这是基于单因变量形式的单变泽尼克系数，泽尼克系数和单项像差的组合都有一些模糊。这个矩阵的组合是首先包括所有的一阶项如(四叶草)Quadrafoil1和（五叶草）Pentafoil1，然后再考虑像散2和彗差2这样的二阶项。上面所示的矩阵也仅限于35个泽尼克系数(z35 max)，即使是复杂的光学系统，这仍然是非常精确的;然而，仍然没有足够的术语显示来描述四叶草Quadrafoil3或五叶草Pentafoil2或3。现在我们可以使用这个矩阵方程，以及复杂光学设计软件输出泽尼克系数，将所有单项像差作为视场角的函数来完全描述。

转换后的单次像差仍然以与泽尼克多项式相同的精度来描述波前，因为单次像差的和是另一个多项式。然而，这个多项式集并不像泽尼克多项式那样正交。与泽尼克多项式不同，对单项求和可以改变峰谷或RMS波前。例如，在“平衡”像差的概念中，在球差或像散的基础上加上离焦可以减少净波前差。

4. WFOV设计实例视场图

下面的图展示了泽尼克多项式和单项多项式在视场依赖性方面的不同。对于一个更简单的近轴透镜设计，差异是微小的。然而，对于更复杂的离轴四镜自由曲面设计，多项式和单项视场图在节点数和弯曲度方面有很大的不同。这是由于四镜设计中的高级像差改变了低阶多项式项。这些图也论证了在更复杂的设计中像差节点数量的增加。

对于图1所示的鱼眼镜头，泽尼克多项式vs视场图如图5所示，泽尼克单项vs视场图如图6所示。图上的圆表示泽尼克曲线通过零像差的位置，因此是一个节点。如前所述，这个节点实际上只表示泽尼克多项式图中的零像差，因为高级像差会干扰泽尼克多项式图中的低阶项。在图5中，我们可以看到泽尼克项大部分随视场单调增加或减少。然而，Z8彗差项

有一个像差项为零的节点。在图6中，“ComaY 1”曲线与图5中的Z8彗发曲线几乎相同。这是因为这种鱼眼透镜没有很强的高阶像差;因此，低阶泽尼克项在描述单个像差时是准确的。

我们可以看到像散Z5曲线开始翻转，但在此视场限制下并没有回到零。低阶项Z4-Z12具有预期的最大值，因为该透镜没有高阶非球面(或自由曲面)表面。正如前面解释的，在这张图中显示的，由于透镜的轴对称，许多泽尼克项为零。一些项(Z4聚焦，Z11球差，Z22球差2)从一个非零像差，预先估计这些项作为主像差视场是不变的。

现在我们来看看图1中更为复杂、两侧对称的四镜设计。本设计的泽尼克多项式vs视场图如图7所示，泽尼克单项与视场图如图8所示。如前所述，由于四镜设计是双边对称的，波前可能存在任何泽尼克项。由于双侧对称，像差类型较多(例如:W12101线性像散或W03001水平彗差)。所以在轴上(零视场)，波前形状(如彗差)有一个有限值，通常在轴上为零。然而，轴上的波前形状必须像光学系统一样是双边对称的。我们可以看到，像Z5和Z8这样的项在轴上为零。这些项在自由曲面上也是零，否则它们将打破双边对称。在图7中，ZvF曲线的形状更为复杂，只能用一个高阶多项式来拟合。由于像差在光学系统内独立影响，ZvF曲线和节点位置之间通常没有重叠。泽尼克低阶项Z4-Z8的ZvF曲线空间频率均随视场的增大而增大。

与鱼眼设计不同的是，四镜设计图7中的泽尼克多项式与图8中的泽尼克单项曲线有很大的不同。这是预料之中的情况，因为四镜设计有更高阶像差，干扰低阶泽尼克多项式项。因此，对于四镜设计，只有泽尼克单项图是准确的确定像差节点。泽尼克单项图的节点一般较少。

下面的表2给出了鱼眼透镜和四种镜面设计中每个泽尼克单项像差的节点数。正如前面提到的，由于鱼眼透镜的对称性和这里使用的x视场，泽尼克的一些项对鱼眼镜头来说是零。然而，由于泽尼克的双侧对称，自由曲面四镜设计可以对任何泽尼克单项具有非零值。这表明鱼眼设计对于每个像差在节点数量上没有超过一个，而且大多数像差没有节点。然而，对于四镜设计，有更多的节点，AstigY1有五个节点。

5.结论

本文提出了一种将单变量泽尼克多项式转换为单项矩阵方法，这对于光线追踪模型中复杂光学设计的像差节点的测量是至关重要的。该方法适用于两种不同的光学设计:(1)120度圆形FOV鱼眼镜头和(2)120×4度矩形FOV、离轴、自由曲面四镜设计。两种设计均为f/3, EFL为2.6英寸。结果表明，在鱼眼透镜中，泽尼克多项式和泽尼克单项式与视场图在拐点和节点位置方面是相似的。然而，在离轴、自由形状的四镜设计中，泽尼克多项式与视场图比泽尼克单项式与视场图有更多的拐点和节点。因此，人们可以从泽尼克多项式和单独的视场图中推断出假节点。四镜设计也比鱼眼透镜有更多的单次像差节点，这是由于它的自由镜面和更高级像差。希望本文能对复杂光学系统中的初级像差和节点与视场的关系有更深入的了解。