结合田口与模糊方法,将液体镜头的微型变焦光学优化设计延伸

摘要：

       在本文中，采用田口方法与模糊方法相结合，为具有液体组件的微型2.5×变焦折光学的多目标设计寻找扩展优化。相对照度（RI）和数据传输函数（MTF）被认为是优化的。对实验进行了模拟，并用光学软件工具 CODE V 对实验结果进行了评价。结论认为，本研究采用的方法在优化值方面是成功的。在所提出的方法中，模糊控制器输入的MTF和RI的适当权重使MTF增加了9.92%，但RI在系统广角端分别减少了0.19%。

1.  介绍

        微型变焦镜头已广泛应用于许多先进的光学系统，如手机摄影、投影系统、显微镜等。现代光学结构采用复杂的整体系统，体积较小光学技术在未来将发挥作用，但传统的复杂机械凸轮系统变焦方法在总长度方面有其局限性[1]。

        镜头体积小的目标可以通过光路径的曲折方式实现，而棱镜中的折射和反射表面则巧妙地组装在一起。U 型 [2] 或 L 型 [3] 镜头就是这样的设计。但是，在设计 U 型或 L 型镜头时，x 方向的总长度小于同轴镜头 [4]。（根据参考。[2，3]，x方向的总长度为15.5毫米和11.36毫米，小于同轴透镜18毫米的总长度。此外，液体镜头在最小化光学变焦镜头的总长度方面也发挥了重要作用[5[8]。根据[3，8]，它可发现x方向的总长度分别是10.10毫米和11.36毫米，y 方向的总长度分别是 23.80 mm 和 24.06 mm。我们可以发现，使用液体镜头的变焦镜头的总长度最小化优于不带液体镜头的变焦镜头。 虽然光学设计的先例方法可以减少体积大小，但也给光学性能带来了一些问题。

         在光学性能方面，调制传输函数（MTF）和相对照度（RI）一直是光学设计中最为熟悉的。MTF 图的纵坐标给出了 MTF 值，这实质上是区分白线和黑线的能力（如图 1 所示）。RI 用于评估从角到中心的光的亮度。由于U型或L型变焦镜头棱镜中的光线通过折射和反射表面，位置1（广角）最大场的RI值将低于一般标准。（根据 [8]，最大字段（在系统广角端）的 MTF 和 RI 分别为 38% 和 61%。

   对于数码相机，最低 （MTF） 和 （RI） 值应超过 40%和 50%，100 lp/mm [4]。但是，如果我们修正了设计以提高 MTF 的值，则 RI 值将相对降低。位置 1（广角）最大场的 MTF 和 RI 值无法产生更好，必须同时改进。这就是所谓的多目标优化问题。

         对于优化 MTF 和 RI 值的多重目标问题。我们的团队将具有强健的多重标准优化 （RMCO） 的 田口(Taguchi) 方法应用于多个响应案例 [8]。在这种方法中，Pareto 优化设计解决方案将由单个 MTF 和 RI 响应的单独 ANOVA 表与约束函数相结合获得。帕雷托 (Pareto) 最佳设计解决方案将包括几组具有不同设计参数的组合，我们可以找到 Pareto 最佳设计解决方案的最佳参数组合，必须由用户判断选择。

        我们发现，在该方法使用时，如果不存在较高的贡献控制因子，则多目标优化的效率将不显著。此外，还开发了田口方法和主要组件分析 （PCA） 方法的集成，以处理多个客观的产品设计问题 [3]。在这种方法中，可以找到控制因子和水平的最佳组合，但如果第一个主组件的特征值小于 1，则最佳设计参数的效果不会显著 [9]。

       为消除上述方法的缺陷，本文提出了一种将田口方法和模糊理论结合在一起的混合方法，在图像光学实验中对多种质量特性进行扩展优化，并结合液体透镜进行L型折迭光学2.5×变焦透镜光学设计作为优化样本。在第 2 节中，我们演示了液体透镜的物理见解以及折迭光学变焦透镜系统的光学设计方法。第3节介绍了田口方法和模糊方法。第4节第5节介绍了优化多种性能特性和实验结果的策略，第6节给出了结论。

2.折迭光学变焦透镜系统的液体镜头的物理内涵和光学设计

       本文参考了L型变焦镜头的设计目标和性能[4]，并采用本组[8]的方法开发结构。L型变焦镜头由光学设计软件 CODE V 设计。L型变焦镜头系统，一个棱镜和两个液体镜头（液体镜头包括两个不同的折射率，它的优点是涉及一个不太移动的组）组装在非同轴光学系统中，这个2.5×微型变焦光学的移动组是两个移动组，可以很好地适用于手机（微型变焦光学可以应用于像手机，视频内窥镜）。

    CODE V 的优化方法是阻尼最少平方 （DLS）。用模糊方法对田口方法初始条件的一些设计参数（即CODE V的优化结果）进行了修正，以改进MTF和RI值。

表 1 中显示了初始设计目标（参考 [4]并进行了一些修订）和光学性能结果（通过 CODE V 的阻尼最少平方）。前镜头的直径为 8.46 mm，后镜头的直径为 5.5 mm。x方向的总长度为10.1毫米，y方向为23.8毫米。2.5×变焦镜头光学设计与液体镜头在优化过程中得以制造，因为制造限制，如前部和后镜头组件的直径。折迭光学变焦系统见图2。

图3和图4显示了变焦镜头在广角位置的性能，显示了MTF的响应和失真。最大字段的 MTF 等于或超过 38%;失真特性分别小于或等于4%。

空间频率的函数有不同的MTF曲线，如图3所示;虚线和实线分别表示子午和切线 MTF。

3.田口法与模糊逻辑法

        田口方法使用正交阵组来执行实验和分析结果。正交数组由内行和外行组成，前者指定控制因子，后者指定输入信号和噪声因子。田口方法的原理是允许设计因子对位于数组外行的噪声因子进行测试，以便优化的控制因子在消除噪音因素对产品质量的影响。

        模糊逻辑是一种不精确的推理数学理论，它允许用语言术语[10]来建模人类推理的过程。它非常适合定义系统输入和所需输出之间的关系。模糊控制器和模糊推理在非常复杂的工业系统中找到了特定的应用，这些应用无法精确建模（系统无法精确建模意味着系统不能或不需要用数学建模），即使在各种假设和近似下。模糊系统主要由模糊器、推理引擎、数据库、规则基和模糊器组成。在研究中，模糊化器首先使用其成员函数将清脆输入转换为模糊集，然后推理引擎对模糊规则执行模糊推理以生成模糊值，然后模糊化器将这些值转换为清晰输出。

       模糊值由成员函数确定，该函数定义模糊集 [11] 中对象的成员资格程度。但是，到目前为止，还没有为控制变量的模糊集选择成员函数的正确形状的标准方法。通常采用试验和错误方法。基于模糊规律，本研究采用曼达尼含意法(Mamdani implication Method)进行模糊推理。典型的规则是 [12]：

其中 M 是模糊规则的总数，xj （j = 1，2,. . . . s） 是输入变量,  yi 是输出变量，Aij 和 Ci 是分别由成员函数 _Aij （xj） 和 _Ci （yj） 建模的模糊集。基于一组分离规则的Mamdani暗示推理方法，M规则的聚合输出为：

上面的方程如图5所示。本文的成员资格功能见图 6 和 8。成员资格函数使用三角成员函数。该图表示两个规则 R1 和 R2 的模糊推理过程，其中两个输入变量（本文中的两个输入变量 PC1 和 PC2 如图 7 所示），它们使用三角形成员资格函数。使用模糊化方法，模糊值可以组合成一个清晰的输出值。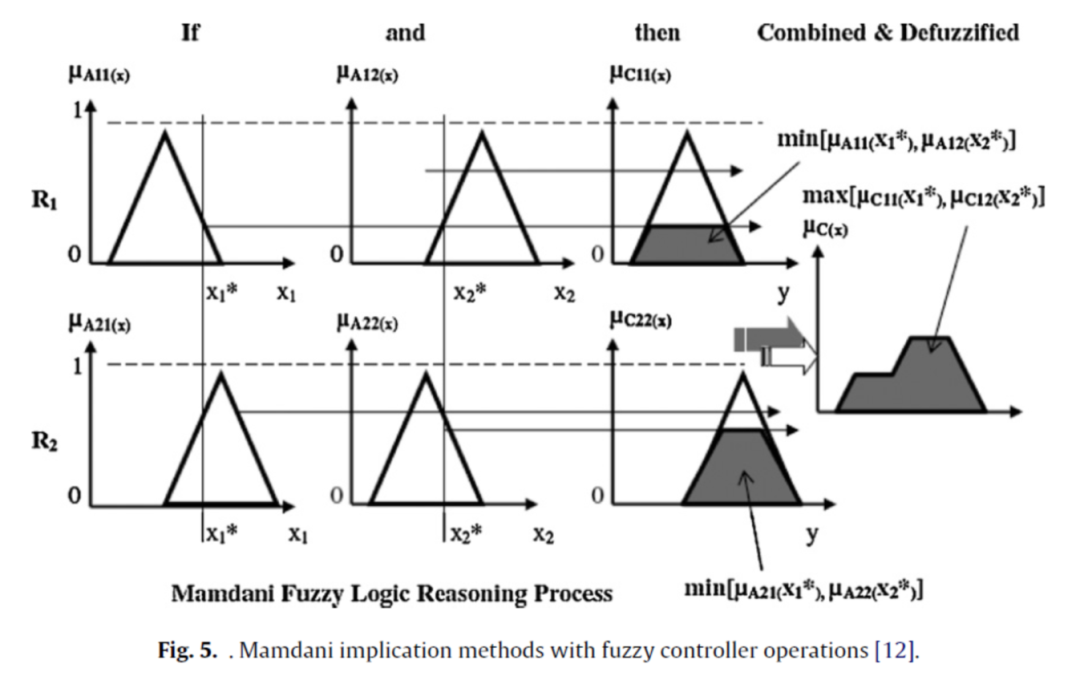

重心是模糊输出函数 除模糊 最流行的方法之一，本研究采用重心。找到组合输出的质心 ˆyi的公式由以下公式给出：

所得值是从输入变量中获得的最终清晰的输出值。本文的最终清晰的输出值是多个性能特征指针。

4. 优化多种性能特性的策略

         本研究采用田口方法进行实验和分析，可以缩短实验时间，获得最大效果。因此，我们可以获得非常准确的结果，而无需进行完整的因子实验。（田口方法只能应用于单个性能质量特性 [13]。模糊方法可应用于多个性能质量特征（从输入变量中获得的多重性能特性指针）。田口方法，结合模糊逻辑分析的L型变焦镜头的多个性能特征（MPC）优化与液体组件，它由以下步骤组成：

1。选择正交数组L9作为起点

2。将每个质量特征转换为 S/N（表 4），然后规范化（表 5） 

3。设置输入输出和模糊规则 的成员函数。

4。开始计算模糊控制器（模糊推理、模糊化接口）

5。计算多个效能特征指数 （MPCI） 

6。对主要分量点进行方差分析（ANOVA），绘制MPCI响应表和图，以找到最佳参数组合

7。执行确认测试

5. 实验结果

5.1. 系统性能评估和常态化

        根据参考文献[8]，连同备选水平，确定了四个主要设计参数，作为控制因素列在表2中。噪声系数及其替代水平列在表 3 中。本研究中，MTF 和 RI 被选为系统的性能特征，其中值越大，系统性能越好。

根据 [14]，选择了更好的 S/N 比率。它可以计算为：

         其中S/N用于计算模拟噪声强度，因此其单位以分贝 （dB） 为单位。无论 S/N 具有什么特性，变化较少的 S/N 值多，与质量更高相对应。yi 表示 MTF 和 RI 的值。

         表4列出了L9的完整实验布局和MTF和RI的S/N比。在执行模糊逻辑分析之前，初始数据（S/N 比率的结果）必须在 0 和 1 之间进行规范化，以避免忽略较小的范围。在这项研究中，xi（k）是MTF和RI的S/N值，k是MTF和RI，必须由Eq.（4）进行规范化，0表示最差性能，1表示最佳。例如，MTF 的 x1 为 +6.228 （表 4），最大值 xi （MTF） 为±5.953，最小 xi （MTF） 为 +6.322，_x1（MTF） 为 0.254。规范化的数据见表 5。

表 5 列出了 MPC 性能评估在 0 到 1 之间的规范化。

5.2. MPCI的模糊逻辑分析

        为了便于使用液体组件对L型变焦镜头进行MPC优化，可以使用模糊输入成员函数进一步将PC分数作为MPC指数（MPCI）的PC总分进行集成，如图6所示。由于PC分数对总方差具有类似的解释能力，因此它们都包含在模糊推理过程中。如图 7 所示，模糊逻辑控制器具有两个处理单元和一个输出。PC1 和 PC2 充当 MPCI 值的最终总计单元的输入变量。图8说明了模糊逻辑单位输出成员函数。

       如图 6 和图 8 所示，输入变量有两个模糊集：小 （S）、中 （M） 和大 （L）和 5 个输出：小 （S）、中小型 （SM）、中 （M）、中 （M）、中大 （ML） 和大 （L）。用于模糊逻辑控制器的矩阵形式的模糊规则见表 6。将两个输入变量模糊化为适当的语言值后，将表 6 中的逻辑规则与 Mamdani 推理一起推波，将生成输出 MPCI 值的模糊语言值及其成员数值。MPCI 值反复将输入 （PC） 放入模糊逻辑控制器以计算最终的 MPCI。三角形的位置指示每个输入/输出值的已确定模糊集。每个三角形中变暗区域的高度对应于此模糊集的模糊成员值。应用表 6 中列出的模糊规则，9 个测试中每个测试的计算 MPCI 的所有结果都显示在表 7 中。 

模糊控制器输入的权重与 MTF 和 RI 相等。然后，按照方法步骤操作：

1. 设置输入和输出的成员函数（如图 6 和图 8 所示）和 Matlab 的模糊规则（如表 6 所示）。

2. 将 PC1（± 0.254 × 1）和 PC2（± 0.129 × 1）输入模糊逻辑控制器。

3. 开始计算模糊控制器 （模糊推理、模糊化接口）

4.计算多个性能特征指数（MPCI = 0.303，见表 7）。

5.3. 控制因素对MPCI的影响 

       表7中的MPCI可以通过计算其平均值进一步转化为每个控制因素对MPCI的影响，如表8所列。

       工程系统的实验误差。"最大=最小"范围方法，就其部分而言，表现出整个范围的效果。通过表9的变化分析，每个控制因子对多个性能特性的影响变得明显。A和C因素的贡献占MPCI总差异的近83.98%。B和D因素的贡献占MPCI总差异的近16.02%。这一观察与表8和图9中反映的趋势非常相似。

5.5. 镜头设计的MPC优化 

         镜头的目标是在带液体组件的L型变焦镜头中引入MPC优化。一般来说，许多战略和技术被用来增加MPCI的价值。根据田口方法，可以通过使用MPCI的响应表和图表确定最佳条件。如表 8 和图 9 所示，导致最大 MPCI 的单个控制因子水平为 A3（表面 1 到表面 5 长度：5.1 mm）、B1（表面 7 到图像长度：19.3 mm）、C3（前组件的半孔径：4.5 mm）和 D3（棱镜玻璃材料：BAK4）。初始和最佳条件的绩效评估见表 10。

5.6. MPCI预测最佳参数设计 

       L 型变焦镜头的最佳设计与研究中的液体组件组成因子水平，使 MPCI 值最大化。可以使用添加剂定律预测这两种性能的最佳 MPCI 值，如下所示 [15]： 对于最佳条件：A3B1C3D3

        至于初始条件，A2B2C2D2，MPCI的预测方式相同，如

        其中MPCIaverage代表整体控制因子的平均影响。可以看到，最佳条件的MPCI值比初始条件增加约0.49。

5.7. 确认运行 

        与初始设计相比，优化的参数设计能够将 MTF 提高 0.85 dB，将 RI 降低 0.02 dB，如表 10 所示。此外，优化参数的确认优于初始参数的确认。

5.8. 稳健分析

       为了比较初始条件和最优条件的健全性，检查了初始条件和最优条件的标准偏差，发现MTF最优条件的标准偏差分别降低了10.05%和RI提高了0.13%。根据 [16] 我们使用概率密度函数比较初始条件和最优条件的强健效应。概率密度函数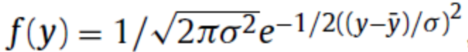 

的结果，其中是σ标准偏差，π是3.142，e = 2.718，

表示平均值（绿色是最佳条件，蓝色是初始条件）如图 10 所示。表11和图10说明，最佳设计可以有效地减少变异，因此，最优设计结论是稳健的。

6. 结论

         与商用光学软件的优化相比，田口和模糊方法的扩展优化对于研究中使用的液体组件的L型变焦镜头具有以下优点：

1. 三个变焦位置的MTF平均消除9.92%，RI为±0.19%，如表11所示。

2. 本研究中获得的参数的最佳组合，可以解决RMCO方法的缺陷（当没有较高的贡献控制因子时，对于多目标优化效率不显著）和PCA和模糊方法（当第一个主要成分的特征值小于1时，最优设计参数的效果将不显著）。

3. 与 [4] 相比，通过将田口方法与模糊方法相结合获得的参数的最佳组合是 RMCO 的一组 Pareto 最优设计解决方案，在最短的总长度条件下，其 RI 值（每个场的均值）更好。

4. 从研究和分析中可以得出结论，建议的最佳设计可以减少变异。因此，最佳设计是稳健的。

References

[1] S. Kuiper, B.H.W. Hendriks, J.F. Suijver, I. Deladi, I. Helwegen, Zoom camera

based on liquid lenses, MOEMS and miniaturized systems VI, Proc. SPIE 6466

(2007) 64660F.

[2] J.H. Sun, Y.C. Fang, B.R. Hsueh, J. MacDonald, Study of extended optimization for

U-type 2× zoom optics with free-form surface, Opt. Lasers Eng. 48 (3) (2010)

368–379.

[3] J.H. Sun, B.R. Hsueh, Y.C. Fang, J. MacDonald, Optical design and extended multiobjective

optimization of miniature L-type optics, J. Opt. A: Pure Appl. Opt. 11

(10) (2009) 1–11.

[4] C.C. Hu, Y.C. Fang, H.W. Su, W.T. Lin, H.C. Lin, Y.C. Lin, Chromatic Aberration

Elimination for 3×

Zoom Lens Design with Liquid Lens via Genetic Algorism,

SPIE, Chengdu, China, 2007, July, pp. 1–10.

[5] C.M. Tsai, Y.C. Fang, Miniature lens design and optimization with liquid lens

element via genetic algorithm, J. Opt. A 10 (2008) 075304.

[6] S. Kuipera, B.H.W. Hendriks, Variable-focus liquid lens for miniature cameras,

Appl. Phys. Lett. 85 (2004) 16.

[7] F.C. Wippermann, P. Schreiber, A. Bruer, P. Craen, Bifocal liquid lens zoom

objective for mobile phone applications, Proc. SPIE 6501 (2007) 650109.

[8] J.H. Sun, B.R. Hsueh, Y.C. Fang, J. MacDonald, C.C. Hu, Optical design and multiobjective

optimization of miniature zoom optics with liquid lens element, Appl.

Opt. 48 (9) (2009) 1741–1757.

[9] L.I. Tong, C.T. Su, Multi-response robust design by principal component analysis,

Total Qual. Manage. 8 (6) (1997) 409–416.

[10] T.J. Ross, Fuzzy Logic with Engineering Applications, Wiley, 1995.

[11] V. Cherkassky, F. Mulier, Learning from Data: Concepts Theory and Methods,

Wiley, 1998.

[12] Y.C. Fang, Y.F. Tzeng, S.X. Li, A Taguchi PCA fuzzy-based approach for the multiobjective

extended optimization of a miniature optical engine, J. Phys. D: Appl.

Phys. 41 (2008) 1–16.

[13] J. Antony, Multi-response optimization in industrial experiments using

Taguchi’s quality loss function and principal component analysis, Qual Reliab.

Eng. Int. 16 (2000) 3–8.

[14] P.J. Ross, Taguchi Techniques for Quality Engineering, McGraw-Hill, New York,

1996.

[15] Y.W. Wu, Taguchi Methods for Robust Design, 1st ed., ASME Press, New York,

2000, p. 270.

[16] C.T. Su, Quality Engineering, Chinese Society for Quality, Taipei, Taiwan, 2006.